1.1 Двоичные последовательности
- От разведчика было получено сообщение: 000001100101001. В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы К, А, Н, Р, Т, Б; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| К |
А |
Н |
Р |
Т |
Б |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение: 10000101000001. В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы К, А, Н, Р, Т, Б; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| К |
А |
Н |
Р |
Т |
Б |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение: 000001100101001. В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы П, А, О, Р, Т, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| П |
А |
О |
Р |
Т |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение: 1000100001101. В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы П, А, О, Р, Т, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| П |
А |
О |
Р |
Т |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение: 000011000111. В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы П, А, О, Р, Т, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| П |
А |
О |
Р |
Т |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение: 1010100001100.В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы П, А, О, Р, Т, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| П |
А |
О |
Р |
Т |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
00010010000101101
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы А, О, Р, К, Д, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| А |
О |
Р |
К |
Д |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
1010010100111000
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы А, О, Р, К, Д, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| А |
О |
Р |
К |
Д |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
1100110000101000001
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы К, А, Н, Р, Т, Б; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| К |
А |
Н |
Р |
Т |
Б |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
000001101001100001000101001
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы К, А, Н, Р, Т, Б; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| К |
А |
Н |
Р |
Т |
Б |
| 000 |
001 |
01 |
100 |
101 |
11 |
1.2 Символьные последовательности
- От разведчика было получено сообщение:
!!!!!??!!??
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы Ц, И, Т, Р, А, К; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| Ц |
И |
Т |
Р |
А |
К |
| !!! |
!!? |
!? |
?!! |
?!? |
?? |
- От разведчика было получено сообщение:
!!!!!??!!!!??!???
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы В, О, Д, Р, Т, А; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| В |
О |
Д |
Р |
Т |
А |
| !!! |
!!? |
!? |
?!! |
?!? |
?? |
- От разведчика было получено сообщение:
?!?!!?!!!???!!
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы В, О, Д, Р, Т, А; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| В |
О |
Д |
Р |
Т |
А |
| !!! |
!!? |
!? |
?!! |
?!? |
?? |
- От разведчика было получено сообщение:
!!!!!?!?!!?!!!!!??!!!!??!?
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы В, О, Д, Р, Т, А; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| В |
О |
Д |
Р |
Т |
А |
| !!! |
!!? |
!? |
?!! |
?!? |
?? |
- От разведчика было получено сообщение:
???!??!!?!????!?!?!!?!!!?!?
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы Ц, И, Т, Р, А, К; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| Ц |
И |
Т |
Р |
А |
К |
| !!! |
!!? |
!? |
?!! |
?!? |
?? |
Тренировочные варианты
Вариант 1
- От разведчика было получено сообщение:
000001100001101
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы К, А, Н, Р, Т, Б; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| К |
А |
Н |
Р |
Т |
Б |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
1100101001101
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы А, О, Р, К, Д, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| А |
О |
Р |
К |
Д |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
!!!!!??!!!!??!?
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы В, О, Д, Р, Т, А; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| В |
О |
Д |
Р |
Т |
А |
| !!! |
!!? |
!? |
?!! |
?!? |
?? |
Вариант 2
- От разведчика было получено сообщение:
0000011100101
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы К, А, Н, Р, Т, Б; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| К |
А |
Н |
Р |
Т |
Б |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
1100101100000
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы А, О, Р, К, Д, Г; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| А |
О |
Р |
К |
Д |
Г |
| 000 |
001 |
01 |
100 |
101 |
11 |
- От разведчика было получено сообщение:
???!??!!?!?!?
В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы Ц, И, Т, Р, А, К; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.
| Ц |
И |
Т |
Р |
А |
К |
| !!! |
!!? |
!? |
?!! |
?!? |
?? |
Ответы
2.1 Двоичные последовательности
1. карта
2. ранка
3. парта
4. ропот
5. порог
6. топор
7. аккорд
8. дорога
9. баранка
10. катаракта
2.2 Символьные последовательности
1. цирк
2. 3. 4. 5. 6. 7. 8. 9. 10.
Тренировочные варианты
Вариант 1. 1. 2. 3. 4.
Вариант 2. 1. 2. 3. 4.

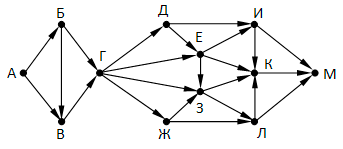
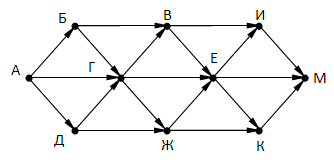
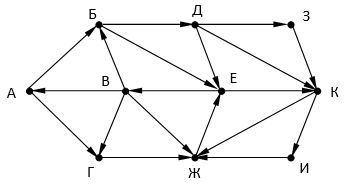
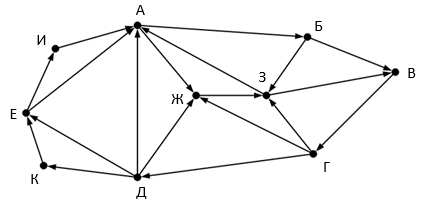
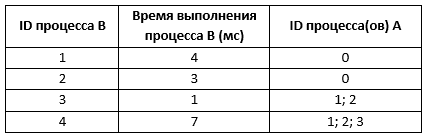
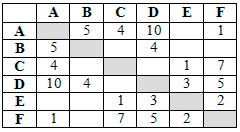
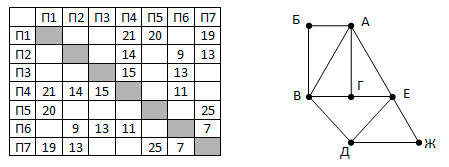
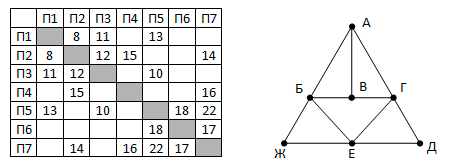
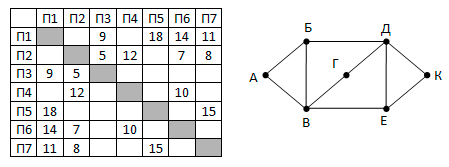
 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите длину дороги между пунктами Г и Е. Передвигаться можно только по указанным дорогам.
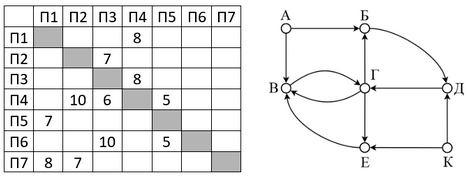
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите длину дороги между пунктами Г и Е. Передвигаться можно только по указанным дорогам.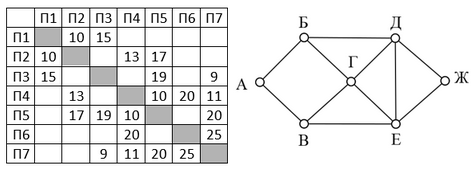 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите длину дороги между пунктами А и Б, если известно, что длина дороги между Г и Д меньше длины дороги между Г и Е. Передвигаться можно только по указанным дорогам.
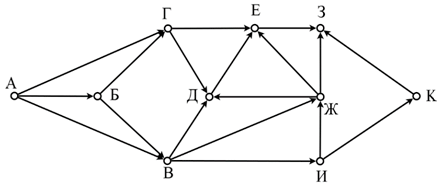
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите длину дороги между пунктами А и Б, если известно, что длина дороги между Г и Д меньше длины дороги между Г и Е. Передвигаться можно только по указанным дорогам.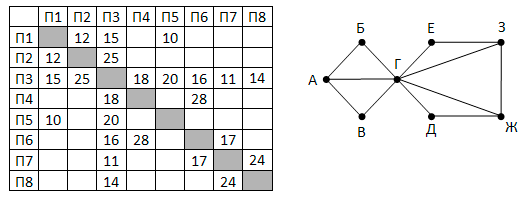 Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину более длинной из дорог ЕЗ и ДЖ. В ответе запишите целое число.
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину более длинной из дорог ЕЗ и ДЖ. В ответе запишите целое число.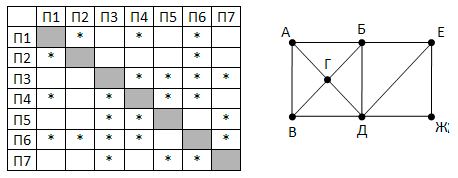 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания, указанные на графе буквенные обозначения пунктов от П1 до П7: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания, указанные на графе буквенные обозначения пунктов от П1 до П7: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.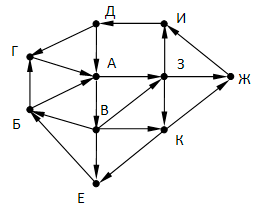

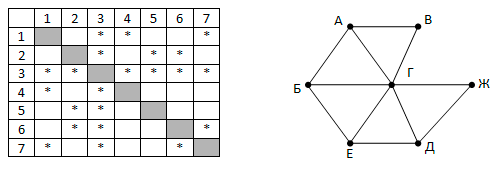
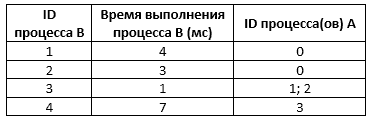
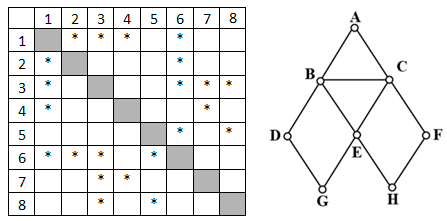
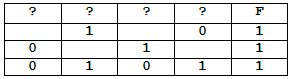
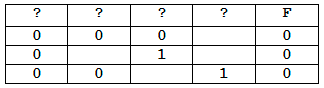 На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.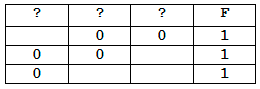 На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c. Пример. Функция F задана выражением x ∨ y ∨ z, а фрагмент таблицы истинности имеет вид:
Пример. Функция F задана выражением x ∨ y ∨ z, а фрагмент таблицы истинности имеет вид: В этом случае переменные можно расставить любым способом, значит, ответом будет число 6.
В этом случае переменные можно расставить любым способом, значит, ответом будет число 6. В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.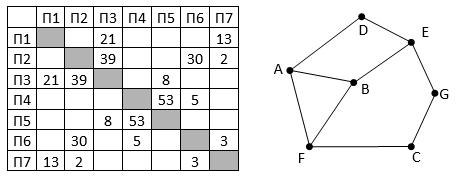
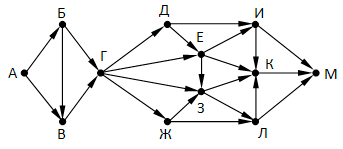
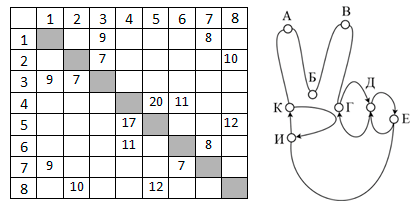 Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего кольцевого маршрута, проходящего через все пункты и оканчивающемся в пункте, из которого было начато движение. Передвигаться можно только по указанным дорогам. В ответе запишите целое число – длину пути в километрах.
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего кольцевого маршрута, проходящего через все пункты и оканчивающемся в пункте, из которого было начато движение. Передвигаться можно только по указанным дорогам. В ответе запишите целое число – длину пути в километрах.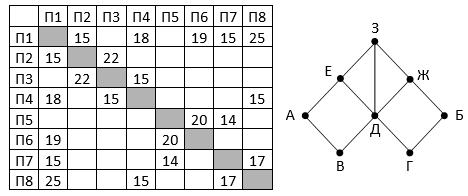
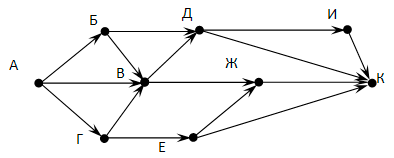
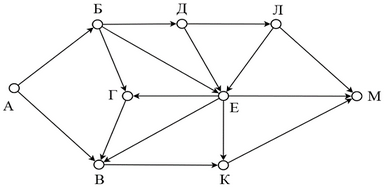
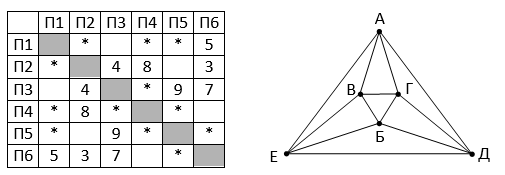 Определите минимальную известную протяженность пути из города А в город Б, состоящего ровно из двух дорог.
Определите минимальную известную протяженность пути из города А в город Б, состоящего ровно из двух дорог.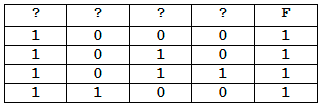


 На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w. В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.